Antimicrobial resistance (AMR) is a global health crisis, and
understanding resistance patterns is crucial for managing effective
treatments. The AMR R package provides robust tools for
analysing AMR data, including convenient antibiotic selector functions
like aminoglycosides() and betalactams(). In
this post, we will explore how to use the tidymodels
framework to predict resistance patterns in the
example_isolates dataset.
By leveraging the power of tidymodels and the
AMR package, we’ll build a reproducible machine learning
workflow to predict resistance to two important antibiotic classes:
aminoglycosides and beta-lactams.
Objective
Our goal is to build a predictive model using the
tidymodels framework to determine resistance patterns based
on microbial data. We will:
- Preprocess data using the selector functions
aminoglycosides()andbetalactams(). - Define a logistic regression model for prediction.
- Use a structured
tidymodelsworkflow to preprocess, train, and evaluate the model.
Data Preparation
We begin by loading the required libraries and preparing the
example_isolates dataset from the AMR
package.
# Load required libraries
library(tidymodels) # For machine learning workflows, and data manipulation (dplyr, tidyr, ...)
#> Error in get(paste0(generic, ".", class), envir = get_method_env()) :
#> object 'type_sum.accel' not found
#> ── Attaching packages ────────────────────────────────────── tidymodels 1.2.0 ──
#> ✔ broom 1.0.7 ✔ recipes 1.1.0
#> ✔ dials 1.3.0 ✔ rsample 1.2.1
#> ✔ dplyr 1.1.4 ✔ tibble 3.2.1
#> ✔ ggplot2 3.5.1 ✔ tidyr 1.3.1
#> ✔ infer 1.0.7 ✔ tune 1.2.1
#> ✔ modeldata 1.4.0 ✔ workflows 1.1.4
#> ✔ parsnip 1.2.1 ✔ workflowsets 1.1.0
#> ✔ purrr 1.0.2 ✔ yardstick 1.3.1
#> ── Conflicts ───────────────────────────────────────── tidymodels_conflicts() ──
#> ✖ purrr::discard() masks scales::discard()
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
#> ✖ recipes::step() masks stats::step()
#> • Use tidymodels_prefer() to resolve common conflicts.
library(AMR) # For AMR data analysis
# Load the example_isolates dataset
data("example_isolates") # Preloaded dataset with AMR results
# Select relevant columns for prediction
data <- example_isolates %>%
# select AB results dynamically
select(mo, aminoglycosides(), betalactams()) %>%
# replace NAs with NI (not-interpretable)
mutate(across(where(is.sir),
~replace_na(.x, "NI")),
# make factors of SIR columns
across(where(is.sir),
as.integer),
# get Gramstain of microorganisms
mo = as.factor(mo_gramstain(mo))) %>%
# drop NAs - the ones without a Gramstain (fungi, etc.)
drop_na() # %>%
#> ℹ For aminoglycosides() using columns 'GEN' (gentamicin), 'TOB'
#> (tobramycin), 'AMK' (amikacin), and 'KAN' (kanamycin)
#> ℹ For betalactams() using columns 'PEN' (benzylpenicillin), 'OXA'
#> (oxacillin), 'FLC' (flucloxacillin), 'AMX' (amoxicillin), 'AMC'
#> (amoxicillin/clavulanic acid), 'AMP' (ampicillin), 'TZP'
#> (piperacillin/tazobactam), 'CZO' (cefazolin), 'FEP' (cefepime), 'CXM'
#> (cefuroxime), 'FOX' (cefoxitin), 'CTX' (cefotaxime), 'CAZ' (ceftazidime),
#> 'CRO' (ceftriaxone), 'IPM' (imipenem), and 'MEM' (meropenem)
# Cefepime is not reliable
#select(-FEP)Explanation: - aminoglycosides() and
betalactams() dynamically select columns for antibiotics in
these classes. - drop_na() ensures the model receives
complete cases for training.
Defining the Workflow
We now define the tidymodels workflow, which consists of
three steps: preprocessing, model specification, and fitting.
1. Preprocessing with a Recipe
We create a recipe to preprocess the data for modelling. This
includes: - Encoding resistance results (S, I,
R) as binary (resistant or not resistant). - Converting
microbial organism names (mo) into numerical features using
one-hot encoding.
# Define the recipe for data preprocessing
resistance_recipe <- recipe(mo ~ ., data = data) %>%
step_corr(c(aminoglycosides(), betalactams()), threshold = 0.9)
resistance_recipe
#>
#> ── Recipe ──────────────────────────────────────────────────────────────────────
#>
#> ── Inputs
#> Number of variables by role
#> outcome: 1
#> predictor: 20
#>
#> ── Operations
#> • Correlation filter on: c(aminoglycosides(), betalactams())Explanation: - step_mutate() transforms
resistance results (R) into binary variables (TRUE/FALSE).
- step_dummy() converts categorical organism
(mo) names into one-hot encoded numerical features, making
them compatible with the model.
2. Specifying the Model
We define a logistic regression model since resistance prediction is a binary classification task.
# Specify a logistic regression model
logistic_model <- logistic_reg() %>%
set_engine("glm") # Use the Generalized Linear Model engine
logistic_model
#> Logistic Regression Model Specification (classification)
#>
#> Computational engine: glmExplanation: - logistic_reg() sets up a
logistic regression model. - set_engine("glm") specifies
the use of R’s built-in GLM engine.
3. Building the Workflow
We bundle the recipe and model together into a workflow,
which organizes the entire modeling process.
# Combine the recipe and model into a workflow
resistance_workflow <- workflow() %>%
add_recipe(resistance_recipe) %>% # Add the preprocessing recipe
add_model(logistic_model) # Add the logistic regression model
resistance_workflow
#> ══ Workflow ════════════════════════════════════════════════════════════════════
#> Preprocessor: Recipe
#> Model: logistic_reg()
#>
#> ── Preprocessor ────────────────────────────────────────────────────────────────
#> 1 Recipe Step
#>
#> • step_corr()
#>
#> ── Model ───────────────────────────────────────────────────────────────────────
#> Logistic Regression Model Specification (classification)
#>
#> Computational engine: glmTraining and Evaluating the Model
To train the model, we split the data into training and testing sets. Then, we fit the workflow on the training set and evaluate its performance.
# Split data into training and testing sets
set.seed(123) # For reproducibility
data_split <- initial_split(data, prop = 0.8) # 80% training, 20% testing
training_data <- training(data_split) # Training set
testing_data <- testing(data_split) # Testing set
# Fit the workflow to the training data
fitted_workflow <- resistance_workflow %>%
fit(training_data) # Train the model
#> ℹ For aminoglycosides() using columns 'GEN' (gentamicin), 'TOB'
#> (tobramycin), 'AMK' (amikacin), and 'KAN' (kanamycin)
#> ℹ For betalactams() using columns 'PEN' (benzylpenicillin), 'OXA'
#> (oxacillin), 'FLC' (flucloxacillin), 'AMX' (amoxicillin), 'AMC'
#> (amoxicillin/clavulanic acid), 'AMP' (ampicillin), 'TZP'
#> (piperacillin/tazobactam), 'CZO' (cefazolin), 'FEP' (cefepime), 'CXM'
#> (cefuroxime), 'FOX' (cefoxitin), 'CTX' (cefotaxime), 'CAZ' (ceftazidime),
#> 'CRO' (ceftriaxone), 'IPM' (imipenem), and 'MEM' (meropenem)
fitted_workflow
#> ══ Workflow [trained] ══════════════════════════════════════════════════════════
#> Preprocessor: Recipe
#> Model: logistic_reg()
#>
#> ── Preprocessor ────────────────────────────────────────────────────────────────
#> 1 Recipe Step
#>
#> • step_corr()
#>
#> ── Model ───────────────────────────────────────────────────────────────────────
#>
#> Call: stats::glm(formula = ..y ~ ., family = stats::binomial, data = data)
#>
#> Coefficients:
#> (Intercept) GEN TOB AMK KAN PEN
#> 101.11641 -3.69738 4.55879 1.86703 -23.37497 -0.57182
#> OXA FLC AMC AMP TZP CZO
#> -4.68575 -11.69742 0.79748 -1.56197 0.87667 -2.28424
#> FEP CXM FOX CAZ CRO IPM
#> -0.19847 0.02659 10.32455 10.27248 0.97321 -0.93096
#> MEM
#> -0.88753
#>
#> Degrees of Freedom: 1573 Total (i.e. Null); 1555 Residual
#> Null Deviance: 2071
#> Residual Deviance: 74.91 AIC: 112.9Explanation: - initial_split() splits
the data into training and testing sets. - fit() trains the
workflow on the training set.
Next, we evaluate the model on the testing data.
# Make predictions on the testing set
predictions <- fitted_workflow %>%
predict(testing_data) # Generate predictions
probabilities <- fitted_workflow %>%
predict(testing_data, type = "prob") # Generate probabilities
predictions <- predictions %>%
bind_cols(probabilities) %>%
bind_cols(testing_data) # Combine with true labels
predictions
#> # A tibble: 394 × 24
#> .pred_class `.pred_Gram-negative` `.pred_Gram-positive` mo GEN TOB
#> <fct> <dbl> <dbl> <fct> <int> <int>
#> 1 Gram-positive 1.07e- 1 8.93e- 1 Gram-p… 5 5
#> 2 Gram-positive 3.17e- 8 1.00e+ 0 Gram-p… 5 1
#> 3 Gram-negative 9.99e- 1 1.42e- 3 Gram-n… 5 5
#> 4 Gram-positive 2.22e-16 1 e+ 0 Gram-p… 5 5
#> 5 Gram-negative 9.46e- 1 5.42e- 2 Gram-n… 5 5
#> 6 Gram-positive 1.07e- 1 8.93e- 1 Gram-p… 5 5
#> 7 Gram-positive 2.22e-16 1 e+ 0 Gram-p… 1 5
#> 8 Gram-positive 2.22e-16 1 e+ 0 Gram-p… 4 4
#> 9 Gram-negative 1 e+ 0 2.22e-16 Gram-n… 1 1
#> 10 Gram-positive 6.05e-11 1.00e+ 0 Gram-p… 4 4
#> # ℹ 384 more rows
#> # ℹ 18 more variables: AMK <int>, KAN <int>, PEN <int>, OXA <int>, FLC <int>,
#> # AMX <int>, AMC <int>, AMP <int>, TZP <int>, CZO <int>, FEP <int>,
#> # CXM <int>, FOX <int>, CTX <int>, CAZ <int>, CRO <int>, IPM <int>, MEM <int>
# Evaluate model performance
metrics <- predictions %>%
metrics(truth = mo, estimate = .pred_class) # Calculate performance metrics
metrics
#> # A tibble: 2 × 3
#> .metric .estimator .estimate
#> <chr> <chr> <dbl>
#> 1 accuracy binary 0.995
#> 2 kap binary 0.989Explanation: - predict() generates
predictions on the testing set. - metrics() computes
evaluation metrics like accuracy and AUC.
It appears we can predict the Gram based on AMR results with a 0.995 accuracy. The ROC curve looks like:
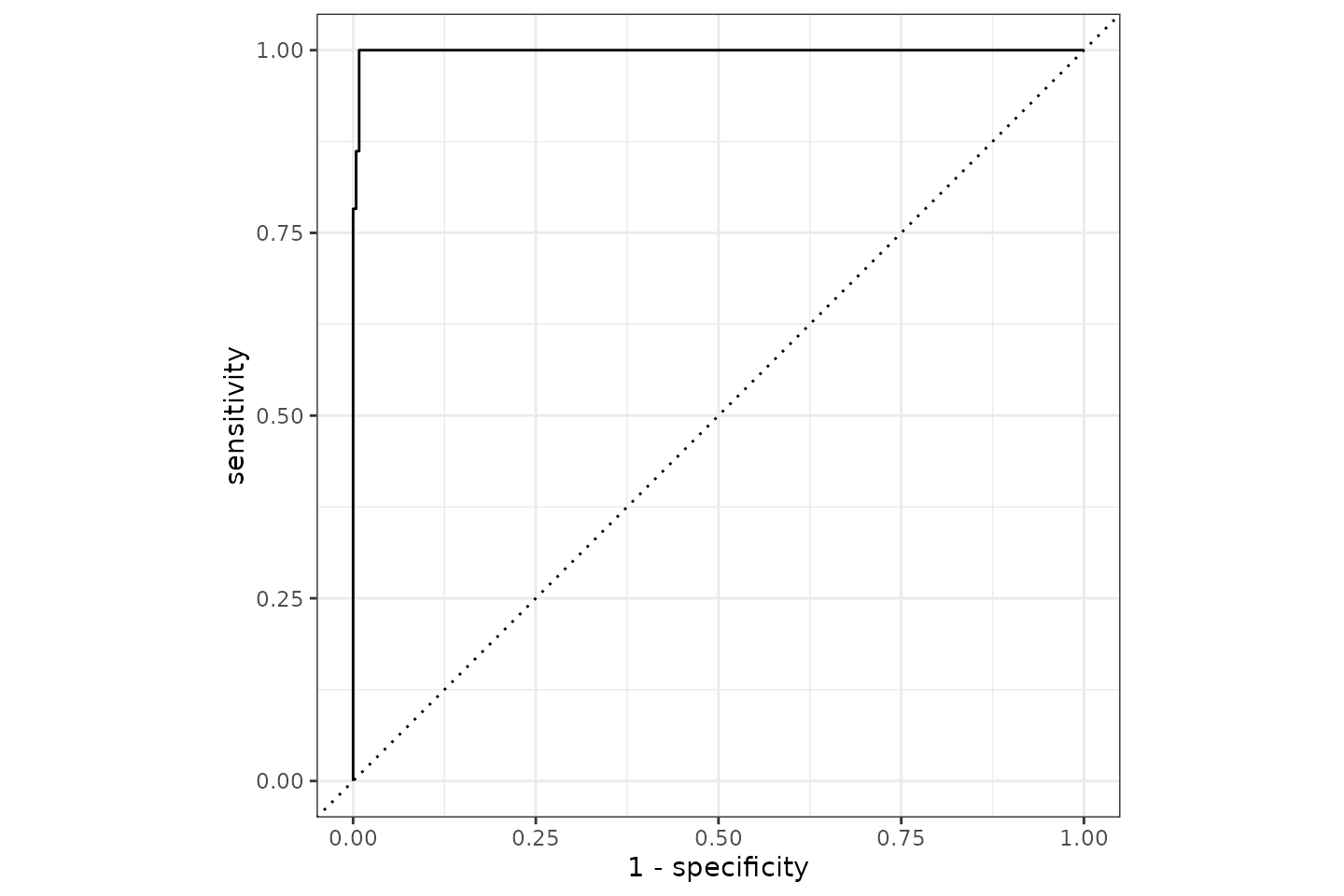
Conclusion
In this post, we demonstrated how to build a machine learning
pipeline with the tidymodels framework and the
AMR package. By combining selector functions like
aminoglycosides() and betalactams() with
tidymodels, we efficiently prepared data, trained a model,
and evaluated its performance.
This workflow is extensible to other antibiotic classes and resistance patterns, empowering users to analyse AMR data systematically and reproducibly.